| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- tonal harmony
- beams
- Augmented
- parallel keys
- triple meter
- tempo
- walking bass
- quadruple meter
- tuplet
- 워킹 베이스
- duple meter
- minor
- relative keys
- figured bass
- 마멘키사우루스
- Inversion
- 역정보
- 갈색과부거미
- copilot
- clef
- lead-sheet symbols
- tonic chord
- 심장박동
- 완화치료
- 전두측두엽치매
- chord substitution
- time signature
- dominant chord
- major scale
- 대리코드
- Today
- Total
트러블해이팅 마인드
Rigid body와 euler angle 본문
어떤 강체가 3차원 공간 상에 존재한다고 하면, 이 강체를 수학적으로 표현하기 위해서는 위치 (position)나 방향 (orientation)을 정의해야만 한다. 위치는 x, y, z 좌표를 이용해 (0, 0, 0)이라고 쉽게 정의할 수 있다. 그런데 방향은 어떻게 정의할 수 있을까? x, y, z의 세 축을 기준으로 회전하면 되지 않을까? 오일러 각 (euler angle)은 3차원 상에서 강체 (rigid body)의 방향과 회전을 정의하기 위해 오일러가 만들어낸 시스템이다. 3차원 공간에 존재하는 어떤 강체를 회전시키고 싶으면 세 개의 축을 통한 회전으로 표현할 수가 있다는 것이다. 다만, 회전을 할 때에는 이 세 축이 종속적일 수밖에 없다. 예를 들어, z축을 돌리는 순간 x, y축은 함께 돌기 때문이다 [1].
1. Construction of a local coordinat system in 3D
· Orientation definition of a segment requires three markers. These three markers describe a plane. In motion analysis, these points can be landmarks or technical markers.
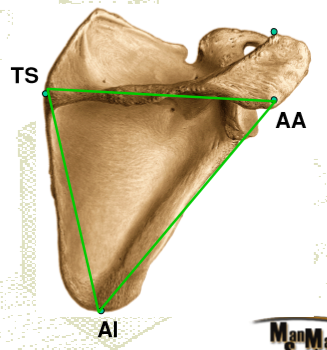
· From x-y-z global coordinates markers, we can construct a local coordinate system (or: frame). Frame describes its orientation and position (=pose) in global space.

· There are five steps to define a local frame
① Define the first axis (ref: latex code https://www.codecogs.com/latex/eqneditor.php)
$$ \bar{z}_{u}=\frac{AA-TS}{\left \| AA-TS \right \|} $$
unit vector를 구하기 위해 벡터 AA-TS를 해당 벡터의 magnitude인 AA-TS로 나누어준다.

② Define a support axis to define the plane orientation
$$ \bar{y}_{temp}=\frac{AA-AI}{\left \| AA-AI \right \|} $$
세 점에 의해 정의된 plane의 방향을 정의하기 위해 임시적으로 벡터 하나를 만들어준다.

③ Define a second axis perpendicular to the plane
$$ \bar{x}=\bar{y}_{temp} \times \bar{z}_{u}, \quad \bar{x}_{u}=\frac{\bar{x}}{\left \| x \right \|} $$
벡터 곱 (vector product; cross product)의 정의에 따라 벡터 x는 벡터 y와 z에 의해 형성된 plane에 수직 (perpendicular)이다.

④ Orthogonize your system: calculate the axis in the plane perpendicular to the first two.
$$ \bar{y}=\bar{z}_{u} \times \bar{x}_{u}, \quad \bar{y}_{u}=\frac{bar{y}}{\left \| y \right \|} $$
1번, 3번 과정으로부터 두 axis인 x축과 z축이 정의되었기 때문에, 이 두 축에 수직이 되게끔 y축을 정의해주면 된다. 역시 벡터 곱을 이용한다.

⑤ Construct the orientation matrix = all three axes / direction vectors
$$ R=\begin{bmatrix} \bar{x}_{u}&\bar{y}_{u}&\bar{z}_{u} \end{bmatrix} $$
세 개의 방향을 정의하는 축으로 구성된 1x3의 orientation matrix을 construct한다.

위 내용을 결과적으로 정리해보면 다음과 같다.

· The resulting 3x3 matrix describes the orientation of a segment in the global system. The matrix contains the three direction vectors. Each direction vector defines the angle of that axis with the three axes of the global coordinate system.
$$ R_{scapula}=\begin{bmatrix}
cos(x,X) & cox(y,X) & cox(z,X)\\
cox(x,Y) & cox(y,Y) & cox(z,Y)\\
cox(x,Z) & cox(y,Z) & cox(z,Z)
\end{bmatrix} $$
[1] https://hoodymong.tistory.com/3
짐벌락과 오일러 각 (gimbal lock, euler angles)
-오일러 각이란? -짐벌락이란? -짐벌락은 왜 생기나? 1. Gimbal 이란? 출처 - [http://ko.wikipedia.org/wiki/%EC%A7%90%EB%B2%8C] 이것이 바로 짐벌이다. 위키에는 단일 축으로 물체가 회전하도록 중심축을 가진..
hoodymong.tistory.com
[2] https://www.stiff-project.eu/fileadmin/biomechanics/lecture02_kinematics.pdf
'공학' 카테고리의 다른 글
| Navigation Toolbox: "Rotations, Orientation and Quaternions" 튜토리얼 (0) | 2023.03.14 |
|---|

