| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 갈색과부거미
- walking bass
- lead-sheet symbols
- 전두측두엽치매
- 역정보
- minor
- tonic chord
- beams
- parallel keys
- 워킹 베이스
- relative keys
- clef
- quadruple meter
- copilot
- tuplet
- Inversion
- duple meter
- 마멘키사우루스
- major scale
- 완화치료
- Augmented
- dominant chord
- tonal harmony
- triple meter
- 대리코드
- 심장박동
- tempo
- figured bass
- chord substitution
- time signature
- Today
- Total
트러블해이팅 마인드
[Chapter 1] The Golem of Prague 본문
* 이 글은 Richard McElreath이 저술한 『Statistical Rethinking: A Bayesian Course with Examples in R and Stan, 2nd edition』 (2019, CRC Press) 을 정리 및 인용한 것임을 밝힙니다.[1] 이 글은 저작권법 제28조에 의거하여 인용한 저작물을 '보도·비평·교육·연구 및 이에 준하는 목적'을 위해 '정당한 범위' 안에서 '공정한 관행'에 합치되게 인용하였습니다.
Statistical golems
1. 저자는 statistical model을 만드는 작업을 Prague에서 유태인들이 골렘을 만드는 작업에 비유하며 설명하고 있다. Statistical golems은 인과를 이해하지 못한다. 다만 association만을 이해할 뿐이다. 그러면서 이미 만들어진 statistical model들만을 이용해서 연구결과를 해석하는 것은 큰 오류라는 점을 지적하고 있다.
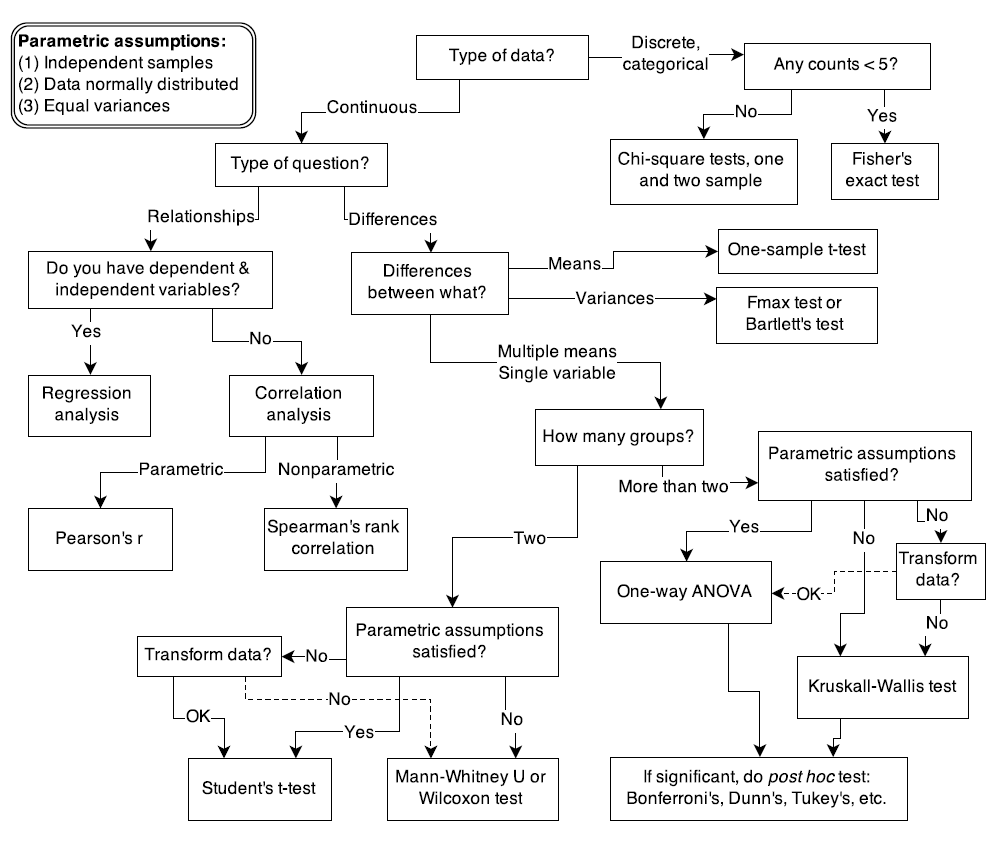
대개의 연구자들은 위와 같은 flow chart를 그대로 적용시켜서 원하는 통계적 방법만을 찾아내곤 한다. 그러나 이런 model을 작동하게 만드는 기저의 principles을 이해하고 큰 그림을 그리지 못한다면, 제대로 통계라는 golem을 이용하고 있다고 볼 수 없다.
아래 현재 과학자들이 하고 있는 일에 대한 저자의 표현이 인상깊어 이를 인용해본다.
"Every active area of science contends with unique difficulties of measurement and interpretation, converses with idiosyncratic theories in a dialect barely understood by other scientists from other tribes."
Statistical rethinking
1. Individual golem과 Statistical epistemology
· golem이 information을 어떻게 처리하는지를 이해하지 못한다면, golem의 output 또한 해석할 수 없다. 그러므로 이 책에서는 각 golem을 구성하는 computational nuts와 bolts를 공부할 것을 주장하고 있다.
· 그러나 학자들이 어떻게 statistical objectives를 정의하였고 statistical results를 해석하는지 이해하기 위해서는 개별적인 golem들만을 이해하는 것을 넘어서 statistical epistemology를 이해할 필요가 있다. 이는 statistical models이 관심있는 hypotheses 및 natural mechanisms과 어떻게 연결되는지에 대한 전체적인 이해이다.
2. 정말 statistical inference의 궁극적 목표는 null hypotheses를 test하는 것일까?
· science는 falsification standard에 묘사되지 않는다. 사실, 거의 모든 과학적 context에서 deductive falsification은 불가능하다. 저자는 두 가지의 이유를 제시하고 있다.
1) Hypotheses are not models.
우선 hypothesis와 model의 개념을 구분해서 알아두어야 한다. 또한 많은 models이 같은 hypothesis와 부합할 수도 있고, 많은 hypotheses가 같은 model과 부합할 수도 있다. 이는 엄밀한 flasification을 불가능하게 만든다.
2) Measurements matters.
설사 우리의 data가 model을 falsify한다 할지라도, 또다른 observer는 우리의 methods와 measures에 태클을 걸 수 있다. 그 observers는 우리의 data를 믿지 않으며, 실제로 그들이 옳을 때도 있다.
위 두 가지에 대해 더 자세히 다루어보자.
2.1. Hypotheses are not models.
· 우리가 어떤 hypothesis를 falsify하려고 시도한다면, 우리는 이에 부합하는 model에 대하여 연구해야 한다. 어떤 hypothesis던 그것을 operationalize하는 model이 항상 있기 마련이기 때문이다. 그렇다면 model을 falsify한다는 것의 의미는 무엇인가? 그것은 해당 model에 대한 기각일 뿐, hypothesis 자체에 대한 기각은 아니다. 아래 그림은 집단 생물학 (population biology)의 context를 예로 든 것이다.
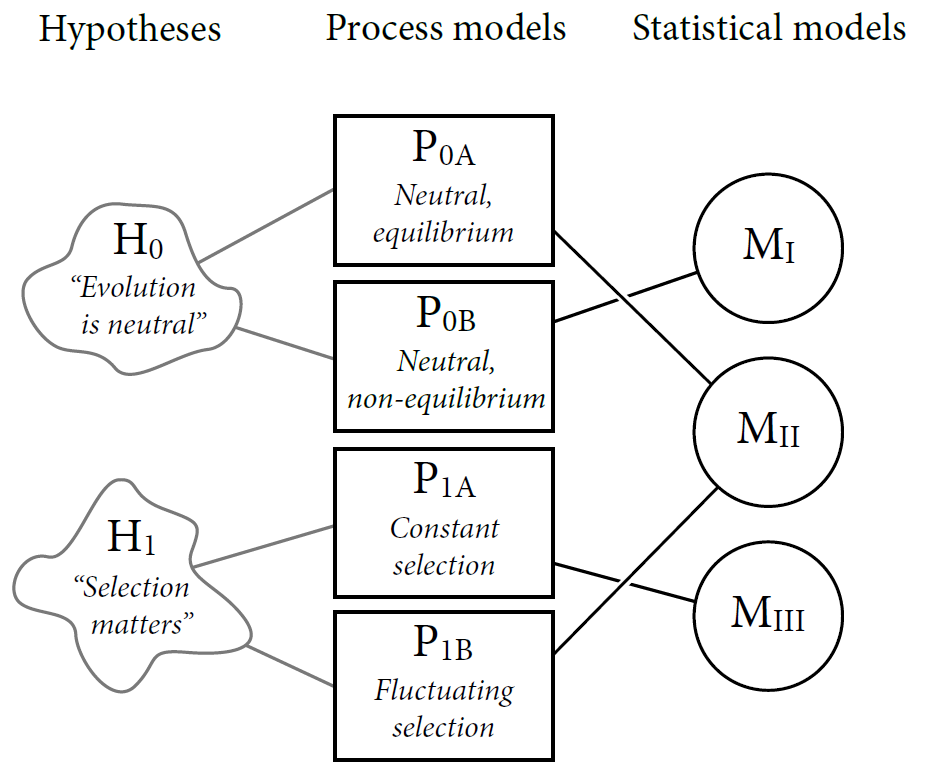
· 가장 왼쪽에는 진화에 대한 두 개의 Hypotheses이 자리하고 있다. 하나는 진화는 "neutral"하다 (H₀)는 것이었고, 하나는 어쨌거나 선택의 문제이다 (H₁)라는 것이었다. 이러한 hypotheses는 단지 verbal conjectures로만 되어 있고 명확한 models이 제시되어 있지 않아 그 boundaries가 매우 모호한 상태이다. 예를 들어 "neutral"하다는 것을 규정지을 상세한 process는 population structure, number of sitres, number of alleles at each site 등 수많을 것이다.
· 이 때 hypotheses를 구체적으로 명시하는 Process models이 등장한다.
- 가설 H₀에 대한 model 두 가지: P₀A의 경우 "population size와 structure이 alleles가 분포되도록 일정하게 유지되어 steady site에 도달한다,"는 내용의 model이다. 다른 하나인 P₀B는 "population size가 시간이 지남에 따라 변하지만 alleles 사이에 selective difference가 존재하지 않는다,"는 내용의 model이다.
- 가설 H₁에 대한 model 두 가지: 매우 많은 가설들이 존재하지만 가장 주요한 두 가지 가설을 소개하고 있다. 하나는 "selection은 언제나 특정한 alleles를 선호하여 이루어진다,"라는 내용이고, 다른 하나는 "selection은 시간이 지남에 따라 변하면서 다른 alleles를 선호하게 된다,"라는 내용이다.
- 이러한 process model의 중요한 특징은 그들의 구조가 casual structure, 즉 인과관계를 표현하고 있다는 것이다. 우리는 이러한 models을 가지고 실험을 수행하여 그들의 casual implications을 조사해볼 수도 있을 것이다.
· data를 이용해 process models을 검증하기 위해, 이들이 Statistical models로 만들어지게끔 해야 한다. 이 때, statistical models 자체는 어떠한 구체적인 casual relationshipss를 포함하지 않는다. 다만 이들은 variables 사이의 assocaitions을 표현할 뿐이다. 그러므로 여러 종류의 다른 process models이 어떤 한 종류의 statistical model을 차용하게 될 수도 있다.
- P₀A와 같은 모델의 경우는 allele frequencies가 power law distribution을 하게 된다. 그러므로 이로부터 data에서 power law를 예측하는 statistical model인 MⅡ가 도출되게 된다.
- constant selection process model인 P₁A의 경우는 이와는 사뭇 다른 MⅢ가 도출된다.
- 또다른 selection models 또한 neutral model과 같은 statistical model인 MⅡ를 암시하게 된다.
· 위 내용들을 종합해보면 아래와 같은 결론을 얻을 수 있게 된다.
① 어떤 statistical model (M)이더라도 한 개 이상의 process model (P)과 부합할 수 있다.
② 어떤 hypothesis (H)이더라도 한 개 이상의 process model (P)과 부합할 수 있다.
③ 어떤 statistical model (M)이더라도 한 개 이상의 hypothesis (H)와 부합할 수 있다.
2.2. Measurement matters.
falsification의 logic은 꽤 단순하다. 우리에게 가설 H가 있고, 이 가설은 observation D와 관련된 내용이다. 그렇다면 우리는 D를 찾는다. 우리가 어떤 D도 찾지 못할 경우 우리는 H가 false라고 결론내릴 수 있다. 논리학자들은 이러한 종류의 추론을 modus tollens라고 부른다. 이는 "the method of destruction"을 라틴어로 표현한 것이다. 이와는 반대로 D를 찾는 것은 H와 관련된 어떤 특별한 것도 이야기해주지 않는다.
이러한 modus tollens를 사용한 유명한 과학적 일화가 바로 swans의 색깔에 관한 이야기이다. Australia를 발견하기 전에 유럽인들은 모든 swans이 흰색 깃털을 가졌을 것이라고 생각했다. 이는 자연스럽게 모든 swans은 희다는 신념으로 자리잡게 되었다. 이것을 formal hypothesis라고 부르자.
H₀: All swans are white.
그런데 유럽인들이 Australia에 당도한 이후 그들은 검은 깃털을 가진 swans를 만나게 되었다. 이 evidence는 가설 H₀이 false라는 것을 즉각 증명했다. 왜냐하면 모든 swans은 흰색이 아니고, 몇몇은 모든 observers가 볼 때도 확실히 검정이었기 때문이다. 여기에 key insight가 있다. Australia로 여행하기 전에는 아무리 많은 수의 white swans을 보았다고 하더라도 그것이 H₀가 true라는 사실을 입증해주지 못했다. 그러나, H₀가 false라는 것을 입증하는 데에는 오직 한 번의 관찰만이 필요했을 뿐이었다.
이처럼 disconfirming evidence를 찾는 것은 매우 중요하다. 그러나 이러한 modus tollens는 swan 이야기에서 보이는 것처럼 그렇게 강력할 수는 없다. 크게 두 가지 이유에서인데 첫째는 observations이 특히 과학적 지식의 경계에서는 error에 취약하기 때문이며, 둘째는 대개의 가설들은 discrete (즉, 있다vs없다)하기보다는 quantitative (즉, a%만큼 존재한다)하기 때문이다.
1) Observation error.
이에 관해서는 두 가지 사례가 있다.
· 첫째는, 코넬 대학의 조류학 연구팀이 멸종된 것으로 알려졌던 Ivory-billed Woodpecker (Campephilus principalis)를 발견했다고 주장한 것이다. 이 때 hypothesis는 아래와 같다고 얘기할 수 있다.
H₀: The Ivory-billed Woodpecker is extinct.
- 그러나 다수의 학자들은 이 disconfirming case에 의문을 제기했다. 그리하여 살아있는 Ivory-billed Woodpecker를 발견하는 사람에게 상금 5만 달러까지 내걸었지만 2015년까지 어느 팀도 만족할만한 evidence를 찾아내지 못했다. 즉, observation이 어렵기 때문에 disconfirming case를 찾는 게 매우 복잡한 것이다. 때로는 black swans이 검은색이 아닐 수도 있고, 때로는 white swans이 진짜 black swans인 경우는 관찰에 매우 어려움을 야기하게 될 것이다.
· 둘째는, 2011년 9월에 물리학 연구팀이 빛보다 빠른 neutrinos를 발견했다는 것이다. 이 때 그간의 hypothesis는 아래와 같다고 얘기할 수 있다.
H₀: Faster-than-light (FTL) particle doesn't exist.
- 그러나 이 때 다수의 학자들은 아인슈타인이 틀렸다는 반응보다는 그 연구팀이 측정을 어떻게 했길래 그런 결과가 나오지? 라는 반응이 대다수였다. 빛보다 빠른 속도의 입자 정도의 속도를 측정하려면 단순히 거리를 시간으로 나누는 방법은 통하지 않는다. 그러므로 statistical model을 사용하게 되는데, 이 때 빛보다 빠르다고 측정했던 것은 이 model로부터의 추정이었던 것이다. 결국 2013년에 물리학회는 FTL neutrino의 발견이 measurement error라는 데에 만장일치로 동의하였다. 이러한 오류는 poorly attached cable에서 연유했다고 한다.
2) Continuous hypotheses.
이는 대개의 과학적 가설이 "all or none"이 아니라 아래와 같은 형태를 띤다는 것이다.
H₀: 80% of swans are white.
혹은
H₀: Black swans are rare.
위와 같은 가설들은 black swan을 관찰한 후에도 기각되지 않는다. 즉, 이러한 종류의 가설은 맞다 틀리다의 문제로 접근할 것이 아니라, 가능한 한 정확히 측정하여 swan coloration의 분포를 설명하는 방식으로 접근할 수밖에 없다는 것이다. 그러므로 이와 같은 문제에는 measurement error가 없다 하더라도 modus tollens를 적용할 수 없게 된다.
3. Falsification is consensual.
falsification은 언제나 consensual하지, logical하지 않다. scientific communities에서는 위에서 언급한 두 가지 문제, 즉 measurement error의 문제와 자연적 현상의 continuous한 nature을 고려하며 evidence의 의미에 대해서 consensus에 다다를 때까지 논쟁하게 된다. 이후에 결과만을 가지고 교과서에서는 logical falsification이라고 설명하곤 하지만, 실제로는 그렇지 않다는 것이다.
Tools for golem engineering
0. 그렇다면 우리가 해야 할 것은?
· 위 session에서는 falsification을 mimic하는 것이 statistical methods에의 유용한 접근 방법이 아니라는 것을 설명하였다. 그렇다면 우리가 하는 것은? 바로 model을 하는 것이다.
· models을 produce하고 manipulate하는 능력은 연구를 하는 데 도움을 준다. 그 이유는 첫째로 scientific problems은 단지 "testing"하는 것보다는 더 general하기 때문이고, 둘째로 통계의 입문 코스에서 배우는 pre-made golems는 다수의 research contexts에 부적합하기 때문이다.
· "Without the engineering training, you're always at someone else's mercy."
· 우리는 우리의 models을 몇 가지 명확한 이유로 사용하고 싶어한다. 즉 inquiry를 design하거나, data로부터 information을 뽑아내거나, predictions을 하거나 등의 목적을 가진다. 저자는 각 목적에 부합하도록 네 가지 도구를 골랐다. 아래의 도구들은 서로 밀접하게 연관되어 있어 함께 다룬다.
1) Bayesian data analysis
2) Model comparison
3) Mutlilevel models
4) Graphical causal models
1. Bayesian data analysis.
우리에게 data가 있다고 할 때, 이를 이용해 어떻게 world에 대해 알 수 있을까? 물론 정답은 없지만, 가장 효과적이고 일반적인 대답이라고 한다면 바로 Bayesian data analysis를 사용하는 것이다.
· Bayesian data analysis는 model의 형식으로 question을 받아들이고, logic을 이용하여, probability distributions의 형식으로 answer을 내놓는다.
· 저자는 bayesian approach와 frequentist approach를 비교하고 있다. frequentist approach는 sampling을 반복하다 보면 data의 pattern이 보일 것이라고 이야기하는 방법론이며, sampling distribution의 형태로 나타나게 된다. 그러나 이는 uncertainity을 묘사하기 위한 유용한 device일 뿐, 우리가 자연 그 자체를 resampling할 수 없기에 현실성은 없는 도구이다. bayesian approach는 이와는 다르게, incomplete knowledge를 가진 상황에서 우리의 uncertainty를 묘사하기 위해 randomness를 이용하는 것 뿐이다.
· "Bayesian data analysis is just a logical procedure for processing information."
2. Model comparison and prediction.
Bayesian data analysis는 models이 data로부터 학습을 하는 방법을 제공한다. 그런데 만약 plausible model이 여러 개라면? 대개 성숙된 분야라면 보통 그러한데, 우리는 그 model 중 어떤 것을 골라야 할까? 우리는 predictions을 잘 하는 models을 고를 필요가 있다. 그렇다면 이것을 어떻게 알 수 있을까? 이 때 Cross validation과 Information criteria라는 두 가지 tools이 등장한다.
· 복잡한 models은 종종 간단한 models보다 더 나쁜 predictions을 내놓는다. 이는 Overfitting (과대적합)이라는 paradox인데, 미래에 입력될 data가 과거의 data와 완벽히 같지 않을 것이기 때문에 지나치게 현재의 data에 적합하게 만든 models의 예측력이 떨어지게 되는 것이다. "the smarter the golem, the dumber its predictions."
· Cross-validation과 information criteria는 우리에게 세 가지 방법으로 도움을 줄 수 있다.
- 첫째는, 그들은 sample에 얼마나 잘 맞는지를 기준으로 하기보다 predictive accuracy에 초점을 맞춘다는 것이다.
- 둘째는, 그들이 model이 data에 얼마나 overfit하는지 그 tendency를 추정한다는 것이다. 이는 models과 data가 어떻게 상호작용하는지 우리로 하여금 이해하게 해 주며, 이는 우리가 더 나은 models을 설계하는 데 도움을 준다.
- 셋째는, 그들은 highly infulential한 observations을 발견하게끔 도움을 준다는 것이다.
3. Multilevel models.
cross-validation과 information criteria는 overfitting risk를 측정하여 우리에게 이를 인식하게끔 해 준다. 그러나 multilevel models은 이에 대해 무언가 중재할 수 있다. 그것이 바로 partial pooling이라고 하는 기법이다.
· 강력한 models은 parameters가 쭉 늘어서 있는 형태이다. 이는, 어떤 특정한 parameter이 missing model의 placeholder로써 여겨질 수 있다는 것이다. 어떤 model에서 그 parameter이 value를 어떻게 얻는지를 알고 있다면, 기존의 model에 새로운 model을 끼워넣는 것은 꽤 간단한 일이 된다. 이는 곧 multiple levels의 uncertanity를 가진 model이 되며, 이것이 곧 multilevel model이다.
· Partial pooling은 모든 units이 더 좋은 estimates를 생산해내게 하기 위해 모든 units의 data안에 들어있는 information을 공유하는 것이다. 아래는 이에 관한 네 가지의 일반적인 사례이다.
1) To adjust estimates for repeat sampling. : 같은 개체, 위치, 시간에 대해 한 번 이상의 observation을 시행할 때, traditional하고 single-level인 models은 제대로 된 결과를 내놓지 못할 것이다.
2) To adjust estimates for imbalance in sampling. : 어떤 개체들, 위치들, 시간들이 다른 것보다 더 많이 sampling되었다면, single-level models은 제대로 된 결과를 내놓지 못할 것이다.
3) To study variation. : 우리의 연구질문이 개체간 혹은 그룹간 data의 variation을 관찰하는 것을 포함한다면, multilevel models이 매우 큰 도움이 될 것이다. 왜냐하면 multilevel models은 명확하게 variation을 model하기 때문이다.
4) To avoid averaging. : 학자들은 꽤 자주 variables를 만들어 regression analysis를 시행하기 위해, 몇몇 data를 가지고 pre-average를 한다. 이는 variation을 없앤다는 측면에서 매우 위험한 행위이다. 그러므로 결과적으로 false confidence를 만들어내게 된다. multilevel models은 original의 uncertainty를 보존하면서도 average를 이용해 predctions을 할 수 있게끔 해 준다.
· "clustered data often often benefit from being modeled by a golem that expects such variation."
4. Graphical causal models.
statistical model은 amazing association engine이다. 이것은 원인과 결과 간의 associations을 탐지할 수 있게 해 준다. 그러나 이것 자체로는 cause를 추론하는데 적합하지 않다. 왜냐하면 statistical model은 바람이 나뭇가지를 흔드는 것과 나뭇가지가 바람을 만들어내는 것을 구별해내지 못하기 때문이다.
· "Models that are causally incorrect can make better predictions than those that are causally correct."
- 즉, cross-validation과 information criteria는 더 잘 예측하는 것을 찾아내는 도구일 뿐이라는 것이다. 이런 도구들은 confounding variables를 포함하거나 잘못된 causal relationships을 암시하는 models을 추천하기도 한다. 왜냐하면, confounded relationships 또한 실제로 존재하는 associations이고 이들이 prediction을 향상시킬 수 있기 때문이다.
- 그러나 이는 우리가 관찰자로 존재할 때에만 유용하다. 무엇이 원인이고 결과인지 알지 못하기에, 우리는 이와 같은 prediction을 가지고 실제로 사람들을 뽑아 나무에 올라 나뭇가지를 흔들어보게 할 수도 있을 것이다. 그러면 바람이 생기는가? 그렇게 많이 생기지는 않을 것이다. 즉, intervention을 하려는 순간 우리는 정확한 causal understanding이 필요하다. 그러나 predictive accuracy에 기반한 models을 비교하는 것만으로는 (p-values나 기타 어떤 것을 사용하더라도) 명확히 무엇이 원인이고 결과인지 알지 못할 것이다.
· 이 때 우리가 필요한 것은 causal identification을 위한 목적으로 하여 한 개 혹은 그 이상의 statistical models을 design하는데 사용될 수 있는 causal model이다. 그러나 완전한 causal model까지도 필요 없다. 어떤 variables이 원인이 되어 다른 것에 영향을 미친다는 heuristic한 model 정도만 있어도 상관없다. 우리는 graphical causal model을 사용하여 causal hypothesis을 대신할 것이다. 가장 간단한 graphical causal model은 directed acyclic graph (DAG)라고 하는 것이다.
Summary
null hypotheses을 테스트하기 위해 다양한 black-box tools 중 하나를 고르는 대신에, 우리는 자연 현상에 대한 다수의 non-null models을 만들고 분석하는 방법을 배워야 한다. 이러한 목표를 달성하기 위해서 우리는 Bayesian inference, model comparison, multilevel models, graphical causal models 등의 방법론을 이번 챕터에서 도입하였다.
1. Chapter 2와 3은 가장 기본적인 내용들이다. 여기서는 Bayesian inference 및 Bayesian calculations을 수행하는 기본적인 도구들을 소개한다. 확률 이론에 대한 완벽히 논리적인 해석을 강조한다.
2. Chapter 4~8에서는 Bayesian tool로써의 다양한 linear regression을 만들 것이다. 이 챕터들에서는 개별적인 parameters의 estimates를 해석하려고 시도하기보다는, results를 plotting하는 데에 초점을 맞출 것이다. 또한 model complexity, 즉 overfitting에 대한 부분도 다룰 것이다. 챕터 7에서는 information theory와 formal model comparison에 대해서도 다룰 것이다.
3. Chapter 9~12에서는 몇 종류의 generalized linear models을 제시할 것이다. 챕터 9에서는 Markov chain Monte Carlo를 소개할 것이며, 챕터 10에서는 models을 디자인하고 해석하는 데 도움을 줄 maximum entropy를 소개할 것이다. 그 후 챕터 11과 12에서 models 자체에 대해 상세히 다룰 것이다.
4. Chapter 13~16에서는 multilevel models과 함께 measurement error, missing data, spatial correlation에 대한 specialized models까지도 다루어볼 것이다. 이 부분은 꽤 advanced한 부분이지만 앞의 내용들과 같은 mechanisitic way로 설명된다. 챕터 16에서는 generalized linear type의 models이 아니라 오히려 statistical models로서 직접적으로 표현되는 theoretical models에 대해 다루어 볼 것이다.
5. 마지막으로 Chapter 17에서는 첫 장에서 다루었던 내용과 같은 issues를 다룰 것이다.
[1] Richard McElreath. Statistical Rethinking: A Bayesian Course with Examples in R and Stan, 2nd edition. CRC Press. 2019:1-18.
'통계 > 『Statistical Rethinking』정리' 카테고리의 다른 글
| [Chapter 2] Small Worlds and Large Worlds (0) | 2019.10.01 |
|---|
